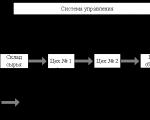
Teorija grafova. Teorija grafova je opsežna neovisna grana diskretne matematike. Koristi se u projektiranju računalnih mreža, cjevovoda, - prezentacija. Grafovi Prikaz grafova i njihove uporabe

Za pregled prezentacije sa slikama, dizajnom i slajdovima, preuzmite njegovu datoteku i otvorite je u programu PowerPoint na vašem računalu.
Tekstualni sadržaj slajdova prezentacije: Grafovi i njihova primjena u rješavanju problema Sadržaj Što je graf Svojstva grafa Povijest nastanka grafova Problem königsberških mostova Primjena grafova Zaključci Što je graf U matematici se definicija grafa daje na sljedeći način: A Graf je neprazan skup točaka i skup odsječaka, čija oba kraja pripadaju zadanom skupu točaka. Točke se nazivaju vrhovima grafa, a spojne linije su bridovi. Bridovi grafa Vrhovi grafa Dalje Što je graf Broj bridova koji izlaze iz vrha grafa naziva se stupanj vrha. Vrh grafa koji ima neparan stupanj naziva se neparan, a vrh koji ima paran stupanj naziva se parni. Sadržaj parnog stupnja Svojstva grafa, zbroj stupnjeva svih njegovih vrhova je paran broj, jednak dvostrukom broju bridova bilo kojeg grafa graf s n vrhova, gdje je n≥2, uvijek postoje dva vrha s istim stupnjevima. Svojstva grafova Ako u grafu s n vrhova (n>2) točno dva vrha imaju isti stupanj, tada u tom grafu uvijek postoji ili točno jedan vrh stupnja 0 ili točno jedan vrh stupnja n-1 graf ima n vrhova, tada će broj bridova biti jednak n(n-1)/2. Svojstva grafa Potpuni graf Nepotpuni graf Svojstva grafa Usmjereni graf Neusmjereni graf Izomorfni grafovi Povijest grafova Pojam "graf" prvi put se pojavio u knjizi mađarskog matematičara D. Koeniga 1936. godine, iako početni najvažniji teoremi o grafovima idu natrag do L. Eulera. Daljnja povijest nastanka grafova Temelje teorije grafova kao matematičke znanosti postavio je 1736. godine Leonhard Euler, razmatrajući problem königsberških mostova. Danas je ovaj zadatak postao klasičan. sadržaj Problem o königsberškim mostovima Bivši Königsberg (sada Kaliningrad) nalazi se na rijeci Pregel. Unutar grada rijeka zapljuskuje dva otoka. Od obala do otoka građeni su mostovi. Stari mostovi nisu sačuvani, ali je ostala mapa grada na kojoj su prikazani. Sljedeći Problem oko königsberških mostova Sljedeći problem bio je široko rasprostranjen među stanovnicima Königsberga: je li moguće prošetati sve mostove i vratiti se na početnu točku, posjećujući svaki most samo jednom? Daljnji problem u vezi s Königsberškim mostovima Nemoguće je hodati preko Königsberških mostova uz poštivanje zadanih uvjeta. Hodanje preko svih mostova, pod uvjetom da svaki treba jednom posjetiti i vratiti se na početnu točku putovanja, jezikom teorije grafova izgleda kao problem prikazivanja grafa “jednim potezom”. dalje Problem Königsberških mostova Ali, budući da graf na ovoj slici ima četiri neparna vrha, nemoguće je nacrtati takav graf "jednim potezom". sadržaj Eulerov graf Graf koji se može nacrtati bez podizanja olovke s papira naziva se Eulerov graf. Rješavajući problem königsberških mostova, Euler je formulirao svojstva grafa: Broj neparnih vrhova (vrhova do kojih vodi neparan broj bridova) grafa mora biti paran. Ne može postojati graf koji ima neparan broj vrhova ako su svi vrhovi grafa parni, tada možete nacrtati graf bez podizanja olovke s papira, a možete početi od bilo kojeg vrha grafa i završiti. na istom vrhu Graf s više od dva neparna vrha ne može se nacrtati jednim potezom. dalje Eulerov graf Ako su svi vrhovi grafa parni, tada možete nacrtati ovaj graf bez podizanja olovke s papira ("jednim potezom"), prolazeći duž svakog ruba samo jednom. Kretanje može započeti iz bilo kojeg vrha i završiti na istom vrhu. dalje Eulerov graf Graf sa samo dva neparna vrha može se nacrtati bez podizanja olovke s papira, a kretanje mora započeti od jednog od tih neparnih vrhova i završiti na drugom od njih. dalje Eulerov graf Graf s više od dva neparna vrha ne može se nacrtati “jednim potezom”. ? Korištenje grafikona Korištenje grafikona pojednostavljuje rješenje matematički problemi, zagonetke, zadaci domišljatosti. dalje Primjena grafova Problem: Arkadij, Boris. Vladimir, Grigorij i Dmitrij su se rukovali kad su se sreli (svaki se rukovao jedan s drugim jednom). Koliko je rukovanja učinjeno? dalje Primjena grafova Rješenje: A D C B D 1 2 3 4 5 6 7 8 9 10 dalje Primjena grafova U državi je sustav zračnih linija osmišljen na način da je svaki grad povezan zračnim linijama s najviše tri druga, a od iz bilo kojeg grada u bilo koji drugi Možete putovati ne više od jedne promjene. Koji najveći broj gradova može biti u ovoj državi? Primjena grafova Neka postoji određeni grad A. Iz njega se ne mogu stići u više od tri grada, a iz svakog od njih u više od dva (ne računajući A). Tada ukupan broj gradova nije veći od 1+3+6=10. To znači da na slici nema više od 10 gradova. Primjena grafova Postoji šahovska ploča 3x3, u gornja dva ugla su dva crna skakača, u donjim su dva bijela (slika dolje). U 16 poteza postavite bijele skakače na mjesto crnih, a crne na mjesto bijelih i dokažite da je to nemoguće učiniti u manje poteza. Primjena grafova Proširivši graf mogućih poteza skakača u krug, nalazimo da su skakači na početku stajali kao na slici ispod: Zaključak Grafovi su prekrasni matematički objekti, uz pomoć kojih možete rješavati matematičke, ekonomske i logičke probleme. Također možete riješiti razne zagonetke i pojednostaviti uvjete problema u fizici, kemiji, elektronici i automatizaciji. Grafikoni se koriste u sastavljanju karata i obiteljskih stabala. Postoji čak i poseban odjeljak u matematici koji se zove “Teorija grafova”. sadržaj

Priložene datoteke

Graf je konačan skup vrhova V i skup bridova R koji povezuju parove vrhova, G=(V,R). Kardinaliteti skupova V i R jednaki su N i M. Skup bridova može biti prazan. Primjeri vrhova su objekti bilo koje prirode (naselja, računalne mreže). Primjeri rubova su ceste, strane, linije.

Vrhovi povezani bridom nazivaju se susjednim. Bridovi koji imaju zajednički vrh nazivaju se i susjedni. Brid i bilo koji od njegova dva vrha nazivaju se incidentom. Stupanj vrha je broj bridova koji mu incidentiraju. Svaki se graf može prikazati na ravnini skupom točaka koje odgovaraju vrhovima, a koje su povezane linijama koje odgovaraju bridovima.

Ruta grafa je niz vrhova i bridova. Ruta je zatvorena (ciklička) ako se početni i završni vrh podudaraju. Ruta je jednostavan lanac ako su svi vrhovi i bridovi različiti. Graf je povezan ako je svaki vrh dostupan iz bilo kojeg drugog. Vrhovi koji nemaju upadne bridove nazivaju se izolirani.

Matrica incidenata

Komunikacijske liste

Popis rebara

Matrica susjedstva grafa povezanog težinskog neusmjerenog grafa

Konstrukcija razapinjućeg povezanog stabla minimalne težine. Kruskalov algoritam Svi bridovi se uklanjaju iz grafa, što rezultira razapinjućim podgrafom gdje su svi vrhovi izolirani. Svaki vrh je smješten u pojedinačni podskup. Rubovi su poredani prema rastućim težinama. Rubovi su uključeni sekvencijalno, rastućim redoslijedom njihovih težina, u razapinjuće stablo.

Postoje 4 slučaja: 1) oba vrha uključenog brida pripadaju pojedinačnim podskupovima, tada se kombiniraju u novi, povezani podskup; 2) jedan od vrhova pripada povezanom podskupu, ali drugi ne, tada uključujemo drugi u podskup kojem prvi pripada; 3) oba vrha pripadaju različitim povezanim podskupovima, tada kombiniramo podskupove; 4) Oba vrha pripadaju istom povezanom podskupu, tada isključujemo ovaj brid.

Primjer konstruiranja razapinjućeg stabla minimalne težine za graf GG Radnje koje treba izvesti Skup vrhova Graf 1 Izgradimo razapinjući podgraf s izoliranim i vrhovima Dobit ćemo 5 podskupova od jednog elementa: (V 1 ), (V 2 ), (V 3 ), (V 4 ), (V 5 ) 2Naći brid minimalne težine (R 15) i dodati ga razapinjućem podgrafu Formiramo povezani podskup vrhova: (V 1,V 5). Spremamo podskupove (V 2), (V 3), (V 4)

Radnje koje treba izvršiti Skup vrhova Grafikon 3 Među preostalima pronađite rub minimalne težine (R 45) i dodajte ga razapinjućem podgrafu. Dodajte vrh povezanom podskupu: (V 1, V 5, V 4 ). Spremamo podskupove (V 2), (V 3) 4 Među preostalim nalazimo rub minimalne težine (R 23) i dodajemo ga razapinjućem podgrafu Formiramo novi povezani podskup vrhova: (V 2, V 3). Spremamo prvi povezani podskup (V 1,V 5, V 4).

Radnje koje treba izvršiti Skup vrhova Graf 5 Među preostalima nalazimo rub minimalne težine (R 25) i dodajemo ga razapinjućem podgrafu Kombiniramo podskupove u jedan povezani podskup (V 1,V 5, V 4, V 2, V 3). 6Preostali rubovi nisu uključeni u graf, jer svi njihovi vrhovi već pripadaju jednom povezanom skupu.

Radnje koje treba izvršiti Skup vrhova Grafikon 7 Dobiven je graf koji je: raspon (svi vrhovi su uključeni); povezani (svi vrhovi mogu biti povezani rutama); stablo (bez petlji); ima minimalnu težinu. 8Rezultirajuće razapinjuće stablo ima minimalnu težinu: R 12 +R 25 +R 15 +R 45 = =80 9 Ciklički broj grafa G je γ=m-n+1=8-5+1=4, što odgovara na broj rubova koji nisu uključeni u stablo.

Deklariranje varijabli Dva niza cjelobrojnih pet elemenata X i Y za pohranjivanje koordinata vrhova grafa Cjelobrojni dvodimenzionalni niz R za pohranjivanje težina rubova grafa Cjelobrojne varijable i, n i k za brojače petlji Cjelobrojna varijabla S za pohranu zbroj težina bridova stabla minimalne težine

Generiranje nasumičnih koordinata 5 vrhova grafa (petlja kroz i). Izračun rubnih težina. Izlaz matrice susjedstva ponderiranog digrafa (ugniježđene petlje po n i po k) Izlaz matrice susjedstva ponderiranog neusmjerenog grafa - polovica elemenata početne matrice (početna vrijednost k=n+1) Tijelo programa

Broj vrhova se naziva
poredak grafa.
Broj bridova se naziva
veličina grafa.

Neki pojmovi-1

- Neka je R=(a,b) jedan od rubova grafa. Zatim
vrhovi a i b nazivaju se krajnjim vrhovima
vrhovi rebra;
- Krajnji vrhovi istog brida
pozvani susjedi;
- Dva brida se nazivaju susjednim ako imaju
zajednički krajnji vrh;
- Dva brida se nazivaju višestruki ako
skupovi njihovih krajnjih vrhova se podudaraju;
- Rub se naziva petlja ako ima krajeve
podudarati se.

Neki pojmovi-2

- Stupanj vrha V označava se s deg(V)
naziva se broj bridova za
od kojih je ovaj vrh terminalni;
- Vrh se naziva izoliranim ako
to nije krajnja točka ni za jednu
rebra;
- Vrh se zove list ako ga
je kraj točno jednog
rebra Za list q očito je deg(q)=1.

Primjer:

stupnjeva(C)=4
H1,…H4 - Lišće

Još jedan primjer:

Gradovi B i D – izolirani
vrhovi; Gradovi G i E su listovi.

Potpuni graf

Graf se naziva potpun ako postoji
dva su vrha povezana bridom.
Koliko bridova ima potpuni graf?
naručiti n?
Kompletan graf reda n ima broj bridova
jednako Cn2=n!/(2*(n-2)!) =n*(n-1)/2

Dokažimo to...

Potpuni graf s dva vrha
sadrži jedan rub - to je očito.
Zamijenite n=2 u formulu n*(n-1)/2
Dobivamo:
n*(n-1)/2=1
Formula je točna kada je n=2

Hipoteza indukcije

Pretpostavimo da je formula točna za
graf s k vrhova.
Dokažimo da ovo implicira
valjanost formule za graf
s (k+1) vrhom.

Dodajmo još jedan vrh kompletnom grafu s K vrhova.

I spojite ga s prvim K
vrhovi...

Dobivamo:

Brojimo koliko smo rebara dobili...

K*(K-1)/2 + K
=
K*(K+1)/2
Posljednji izraz ispada da je
ako je u formuli n*(n-1)/2 umjesto n
zamjena K+1.

Iz pretpostavke pravednosti
iskazi za n=k slijede
valjanost izjave kada
n=k+1.
Teorem je dokazan.

Primjeri kompletnih grafova

Važno pojašnjenje

Parovi koji definiraju rubove u neusmjerenom grafu su neuređeni (tj.
parovi (a,b) i (b,a) se ne razlikuju)

Usmjereni graf

Ako ima mnogo bridova grafa
uređeni parovi (tj. (a,b) ≠ (b,a)),
Tada se graf naziva usmjerenim
(ili digraf)
Kako dati orijentaciju konceptu
vizualno značenje?
Vrlo jednostavno - rebra su priložena
strelice (od početka do kraja)!

Primjer digrafa

Mješoviti graf

Mješoviti graf je trojka (V, E, A).
V – skup vrhova;
E – skup neorijentiranih
rebra;
A je skup orijentiranih bridova.
Usput, orijentirani rubovi
nazivaju se lukovi.

Izomorfizam grafova

Neka postoje dva grafa G1 i G2
Ako postoji korespondencija jedan na jedan F
između vrhova grafova G1 i G2, tako da je:
- ako postoji brid (a,b) u grafu G1, onda postoji i brid u grafu G2
postoji rub (F(a),F(b))
- ako postoji brid (p,q) u grafu G2, onda postoji i brid u grafu G1
postoji rub (F-1(p),F-1(q))
tada se grafovi G1 i G2 nazivaju izomorfnim, i
korespondencija F je izomorfizam.

Pojašnjenje

Za digrafove i mješovite grafove
usklađenost F mora sačuvati
orijentacija lukova.

Nužni uvjeti za izomorfizam

Pod kojim uvjetima između elemenata
dva konačna skupa
uspostaviti jedan na jedan
Dopisivanje?
Tada i samo tada, njihov broj
elementi su isti.
Nužan uvjet za izomorfizam
broj grafova je isti
vrhovi

Je li ovaj uvjet dovoljan?

Ne, jer vrhovi mogu biti
drugačije povezani.

Jesu li ovi grafovi izomorfni?

Broj vrhova je isti -
potreban uvjet je ispunjen...

Pokušavamo izgraditi korespondenciju F...

Ovo nije izomorfizam: G1 ima rub (A,D),
a slike tih bridova u G2 nisu povezane.

Još jedan pokušaj...

A ovo je izomorfizam!

Jesu li ovi grafovi izomorfni?

Nažalost ne…

S teorijskog gledišta, dva
izomorfni grafovi su jedno te isto
isti predmet (samo možda drugačije prikazan...)

Staze (lanci):

Put (lanac) je niz
vrhovi:
a1, a2, … , an
u kojem susjedni vrhovi ai i ai+1
povezani rebrima.
Duljina puta je broj njegovih komponenti
rebra

Primjeri staza:

(A, D, C) i (A, B, D) su staze. (A, B, C) nije način.

Koncept staze za digraf čuva
snaga, ali treba nadopunu -
susjedni vrhovi u
sekvence
a1, a2, … , an
moraju biti povezani lukovima.

Ciklusi

Ciklus je staza koja ima početnu i
konačni vrh se podudara.
Duljina ciklusa je broj njegovih komponenti
rebra
Ciklus se naziva jednostavnim ako su bridovi u njemu
ne ponavljaju se.
Ciklus se naziva elementarnim ako je
jednostavan i vrhovi se u njemu ne ponavljaju.

Komponente povezivanja

Vrhovi proizvoljnog grafa mogu biti
podijeljeni u razrede tako da za
bilo koja dva vrha iste klase v1
i v2 postoji put od v1 do v2
Te se klase nazivaju komponente
povezanost.
Ako graf ima točno jednu komponentu
povezanost, tada se graf naziva
koherentan.

Strojni prikaz grafova.

Matrica susjedstva

- Označimo vrhove grafa G brojevima
uzastopni cijeli brojevi od 1 do n;
- Sastavimo kvadratni n×n stol i
ispunite ga nulama;
- Ako postoji spojni rub
vrhova i i j, zatim na pozicijama (i,j) i (j,i)
isporučit ćemo jedinice;
- Dobivena tablica se zove
matrica susjedstva grafa G.

Primjer

Neka očita svojstva matrice susjedstva

- Ako je vrh izoliran, onda njegov red i
stupac će biti potpuno nula;
- Broj jedinica u redu (stupac)
jednak stepenu koji odgovara
vrhovi;
- Za neusmjerenu matricu grafa
susjedstvo je simetrično u odnosu na
glavna dijagonala;
- Petlja odgovara jedinici koja stoji na
glavna dijagonala.

Generalizacija za digraf

Matrica susjedstva za digraf
može se graditi na sličan način
način, ali voditi računa o redoslijedu
vrhova, možete učiniti ovo:
Ako luk polazi od vrha j i
ulazi u vrh k, zatim na poziciji (j,k)
matrice susjedstva trebaju biti postavljene na 1, a in
pozicija (k,j) set -1.

Matrica incidencije

- Označimo vrhove grafa G brojevima
uzastopni cijeli brojevi od 1 do
n;
- Napravimo pravokutni stol sa
n redaka i m stupaca (kolone
odgovaraju rubovima grafa);
- Ako j-ti brid ima terminal
vrh je vrh k, tada u poziciji
(k,j) je postavljen na jedan. U svemu
u drugim slučajevima je postavljen na nulu.

Matrica incidencije za digraf

- Ako j-ti luk dolazi iz vrha k,
tada se 1 postavlja na poziciju (k,j);
- Ako j-ti luk ulazi u vrh k, tada
-1 postavlja se na poziciju (k,j).
- U ostalim slučajevima u poziciji (k,j)
ostaje nula.

Budući da stupci matrice
incidencija opisuje rebra, dakle
svaki stupac ne smije sadržavati
više od dva elementa različita od nule

Primjer matrice incidencije

Popis rubova

Drugi način predstavljanja grafa
– dvodimenzionalni niz (popis parova).
Broj parova jednak je broju bridova
(ili lukovi).

Primjer rubne liste

Usporedba različitih načina prezentiranja

- Popis rubova je najkompaktniji, i
najmanja matrica incidencije
kompaktan;
- Matrica incidencije je prikladna kada
traženje ciklusa;
- Matrica susjedstva je jednostavnija
ostalo u upotrebi.

Graph Traversal

Obilaženje grafa naziva se njegovim nabrajanjem
vrhova, tako da svaki vrh
pogledano jednom.

Sporazum-1

Prije izvođenja pretraživanja na grafikonu
s n vrhova stvorit ćemo niz Chk
od n elemenata i popunite ga
nule.
Ako je Chk[i] = 0, tada je i-ti vrh miran
nije gledano.

Sporazum-2

Kreirajmo strukturu podataka
(ostava) u kojoj ćemo
zapamtite vrhove u procesu
zaobići. Sučelje za pohranu
treba osigurati tri funkcije:
- Donesite gornji dio;
- Ekstrahirajte vrh;
- Provjerite je li spremište prazno;

Sporazum-3

Kada se vrh j postavi u
skladištenje, označeno je kao
pregledan (tj. instaliran
Chk[j]=1)

Algoritam premosnice-1

1) Uzmi proizvoljan početni vrh,
ispisujemo i čuvamo;

3) Uzmi vrh Z iz memorije;
4) Ako postoji vrh Q povezan sa Z a ne
označeno, zatim vratite Z u pohranu,
staviti Q u pohranu, ispisati Q;
5) Idite na korak 2

Zaobilazni algoritam-2

1) Uzmimo proizvoljan početni vrh i
stavljamo ga u skladište;
2) Je li spremište prazno? Ako DA - kraj;
3) Uzmite vrh Z iz pohrane, ispišite i
izbrisati iz pohrane;
4) Smještamo sve vrhove u pohranu,
Z-povezano i još nije zabilježeno;
5) Idite na korak 2

Koje strukture podataka su prikladne za pohranu?

- Slaganje (PUSH – dodavanje; POP – uklanjanje)
- Red (ENQUE – unesite; DEQUE –
ekstrakt)
Obje strukture omogućuju vam provjeru
dostupnost podataka.

Algoritam-1 u kombinaciji sa stogom
koji se naziva prvo prolaženje po dubini
Algoritam-2 u kombinaciji s redom čekanja
koji se naziva prvi put po širini

1 slajd

2 slajd

Osnove teorije grafova prvi put su se pojavile u djelima Leonharda Eulera (1707.-1783.; švicarski, njemački i ruski matematičar), u kojima je opisao rješavanje zagonetki i matematičkih zabavnih problema. Teorija grafova započela je Eulerovim rješenjem problema sedam mostova u Königsbergu.

3 slajd

Sljedeća zagonetka dugo je bila uobičajena među stanovnicima Königsberga: kako prijeći sve mostove (preko rijeke Pregolya), a da ni preko jednog ne prijeđete dvaput? Mnogi su teoretski i praktično u šetnjama pokušali riješiti ovaj problem. Ali nitko nije uspio, ali ni dokazati da je to čak ni teoretski nemoguće. U pojednostavljenom dijagramu dijelova grada (graf), mostovi odgovaraju linijama (lukovi grafa), a dijelovi grada odgovaraju točkama koje povezuju pravce (vrhovi grafa). Tijekom svog razmišljanja, Euler je došao do sljedećih zaključaka: Nemoguće je prijeći sve mostove, a da se preko bilo kojeg od njih ne prijeđe dvaput.

4 slajd

Postoje 4 krvne grupe. Kada se krv transfuzira s jedne osobe na drugu, nisu sve skupine kompatibilne. Ali poznato je da se identične grupe mogu prenositi s osobe na osobu, t.j. 1 – 1, 2 – 2 itd. Također se grupa 1 može transfuzirati u sve ostale grupe, grupe 2 i 3 samo u grupu 4. Zadatak.

5 slajd

6 slajd

Grafovi Graf je informacijski model predstavljen u grafičkom obliku. Graf je skup vrhova (čvorova) povezanih bridovima. Graf sa šest vrhova i sedam bridova. Vrhovi se nazivaju susjednim ako su povezani bridom.

7 slajd

Usmjereni grafovi - digrafovi Svaki brid ima jedan smjer. Takvi rubovi nazivaju se lukovi. Usmjereni graf

8 slajd

Ponderirani graf Ovo je graf čijim su rubovima ili lukovima dodijeljene numeričke vrijednosti (mogu označavati, na primjer, udaljenost između gradova ili cijenu prijevoza). Težina grafa jednaka je zbroju težina njegovih rubova. Tablica (koja se naziva težinska matrica) ima odgovarajući grafikon. 1 2 4 2 3 A B C D E

Slajd 9

Problem Između naselja Izgrađene su ceste A, B, C, D, E, F čija je dužina prikazana u tabeli. (Nedostatak broja u tablici znači da ne postoji izravna cesta između točaka). Odredi duljinu najkraćeg puta između točaka A i F (pod pretpostavkom da se može putovati samo po izgrađenim cestama). 1) 9 2) 10 3) 11 4) 12

10 slajd

1. 2. 3. 4. 5. Duljina najkraćeg ruta A-B-C-E-F jednako 9 2 4 2 4 7 1 2 4 7 1 3 4 2 4 7 1 3 4 3 2 4 7 1 3 4 3 2